The FoxPro Wiki is down, on purpose
The wiki will stay down until I receive an apology and a personal guarantee from Canadian developer Mike Yearwood that his heinous behavior will stop.
I have zero tolerance for this crap.
Steven Black

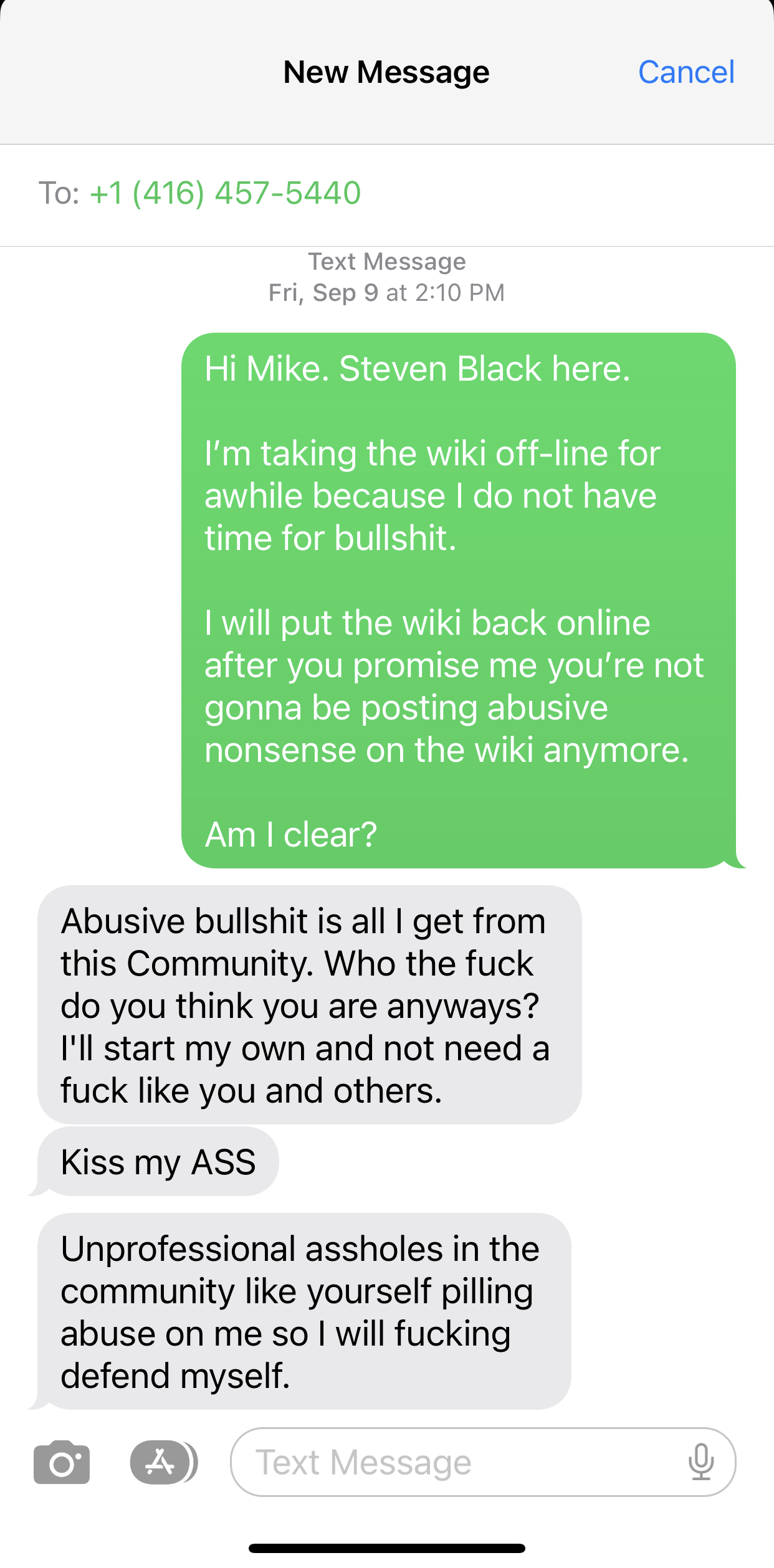
The wiki will stay down until I receive an apology and a personal guarantee from Canadian developer Mike Yearwood that his heinous behavior will stop.
I have zero tolerance for this crap.
Steven Black

